How to write equations in the Graphzapp grapher
Intro
Define equations for x and y in terms of the variable t in order to draw a curve. Include the variable k to allow animation of the curve by sliding the k slider. Graphzapp has several built-in functions including logarithms and trigonometric functions.
Example: In the x= and y= boxes, write equations such as
Arithmetic
Use (+) for addition, (-) for subtraction, (*) for multiplication, (/) for division, and (^) for powers. Use parentheses to group parts of the expressions.
Example: Graph a parabola by typing
Comparisons
Each comparison evaulates to 1 if true and 0 if false. The comparisons are (==) equal to, (!=) not equal to, (<) less than, (>) greater than, (<=) less than or equal to, and (>=) greater than or equal to.
Example:
Boolean Algebra
- Logical AND (&) - returns 1 if both operands are true and 0 otherwise
- Logical OR (|) - returns 1 if either operand is true and 0 otherwise
- Logical NOT (!) - returns 1 when the operand is false and 0 when it is true
When evaluating, anything non-zero stands for true, and only 0 stands for false.
Example:
Function Domains
Graphzapp will not graph any points where the x or y expression is undefined. The expression is undefined if it contains a division by 0, an indeterminate form, or an imaginary answer. Use divison by a boolean expression to limit the domain to only points where the expression is true.
Example:
Piecewise Functions
The (;) symbol lets the expression be definied piecewise. Each part is a value divided by a domain with semicolons (;) separating the parts. At each point, the grapher will draw the first of these parts which is defined when reading from the left, or draw nothing if all are undefined.
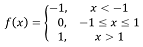
Example: To graph the above piecewise function, we can type